Exercise 2.1
1. The graphs of y = p(x) are in following figure, for some
polynomials p(x) Find the number of zeroes of p(x), in each case.
Answer
P(x) be any polynomial. The number of points that graph of y =
p(x) intesects any x-axis are called zeros of p(x).
(i) Number of zeroes of p(x)
= 0
(ii) Number of zeroes of p(x)
= 1
(iii) Number of zeroes of p(x) = 3
(iv) Number of zeroes of p(x) = 2
(v) Number of zeroes of p(x)
= 4
(vi) Number of zeroes of p(x) = 3
By Kishori Lal-------------------
Page No: 33
Exercise 2.2
1. Find the zeroes of the following
quadratic polynomials and verify the relationship between the zeroes and the
coefficients.
(i) x2 – 2x – 8
(ii) 4s2 – 4s + 1
(iii) 6x2 – 3 – 7x
(iv) 4u2 +8u
(v)
t2 – 15
(vi) 3x2 – x- 4
Answer
(i) x2 – 2x – 8
=(x
– 4)(x + 2)
The value of x2 – 2x – 8 is zero when x – 4 = 0 or x + 2 = 0, i.e
when x = 4 or x = -2
Therefore, the zeroes of x2 – 2x – 8 are 4 and -2.
Sum of zeroes = 4 + (-2) = 2= -(-2)/1
= -(Coefficient of x)/Coefficient of x2
Product of zeroes = 4 x (-2) = -8 =
-8/1 = Constant term/Coefficient of x2
(ii) 4s2 – 4s + 1
= (2s-1)2
The value of 4s2 – 4s + 1is
zero when 2s – 1, i.e., s=1/2
Therefore, the zeroes of 4s2
– 4s + 1 are 1/2 and 1/2.
Sum of zeroes =1/2 + 1/2 =1 = -(-4)/4
=-(Coefficient of s)/Coefficient of s2
Product of zeroes = 1/2 x 1/2 = 1/4 =
Constant term/Coefficient of s2.
(iii) 6x2 – 3 – 7x
= 6x2 – 7x – 3
= (3x +1) (2x – 3)
The value of 6x2 – 3 – 7x is
zero when 3x + 1 = 0 or 2x – 3 = 0., x= -1/3 or x = 3/2
ALSO READ
Therefore, the zeroes of 6x2 – 3 – 7x are -1/3 and 3/2
Sum of zeroes = -1/3 + 3/2 = 7/6 = -(-7)/6 = -(Coefficient of x)/Coefficient of x2
Product of zeroes = -1/3 x 3/2 = -1/2
= -3/2 = -3/6 = Constant term/Coefficient of x2.
(iv) 4u2 +8u
= 4u2 +8u +
=4u(u + 2)
The value of 4u2 +8u is zero
when 4u = 0 or u + 2 = 0, i.e., u = 0 or u = -2
Therefore, the zeroes of 4u2 +8u are 0 and -2
Sum of zeroes = 0+(-2) = -2 = -(8)/4
= -(Coefficient of u)/Coefficient of u2
Product of zeroes = 0x(-2) = 0 = 0/4
= Constant term/Coefficient of u2
(v) t2 - 15
= t2 – 0.t – 15
= (t2 - √15)(t - √15)
The value of t2 – 15 is
zero when t - √15 = 0 or t + √15 = 0, i.e., when t = √15 or t = -√15
Therefore, the zeroes of t2+ -
15 are √15 and -√15. Sum of zeroes = √15 + -√15 = 0
= -0/1 = -(Coefficient of
t)/Coefficient of t2
Product of zeroes = (√15)(- √15) = -15/1 = Constant
term/Coefficient of u2.
(vi) 3x2 – x – 4
= (3x – 4)(x + 1)
The value of 3x2 – x – 4
is zero when 3x -4 = 0 and x+1 = 0,
i.e., when x = 4/3 or x = -1
Therefore, the zeroes of 3x2
– x – 4 are 4/3 and -1
Sum of zeroes = 4/3 +(-1) = 1/3 =
-(-1)/3 = -(Coefficient of x)/Coefficient of x2
Product of zeroes = 4/3 x (-1) = -4/3
= Constant term/Coefficient of x2.
2. Find a quadratic polynomial each
with the given numbers as the sum and product of its zeroes respectively.
(i) 1/4, -1
(ii) √2, 1/3
(iii) 0, √5
(iv) 1, 1
(v) -1/4, 1/4
(vi) 4, 1
Answer
(i) 1/4, -1
Let the polynomial be ax2
+bx + c, and its zeroes be α and β
α + β = 1/4 = -b/a
αβ = -1 = -4/4 = c/a
if a = 4, then b = -1, c = -4
Therefore, the quadratic polynomial is 4x2
– x – 4.
(ii) √2, 1/3
Let the polynomial be ax2 + bx + c,
and its zeros be α and β
α+β = √2 = 3√2/3 = -b/a
αβ = 1/3 = c/a
If α = 3, then b = -3√2, c = 1
Therefore, the quadratic polynomial
is 3x2 – 3√2x + 1
(iii) 0, √5
Let the polynomial be ax2
+ bx + c, and the zeroes be α and β
α + β = 0 = 0/1 = -b/a
αβ = √5 = √5/1 = c/a
if a = 1, then b = 0, c =√5
therefore, the quadratic polynomial
is x2 + √5.
ALSO READ:
(iv) 1,1
Let the polynomial be ax2 +
bx + c, and its zeroes be α and β
α + β = 1 = 1/1 = -b/a
αβ = 1 = 1/1 =c/a
if a = 4, then b = -1, c= 1
Therefore, the quadratic polynomial
is x2 - x + 1.
(v) -1/4, 1/4
Let the polynomial be ax2 +
bx + c, and its zeroes be α and β
α + β = -1/4 = -b/a
αβ = 1/4 =c/a
if a = 4, then b = 1, c= 1
therefore, the quadratic polynomial
is 4x2 + x + 1.
(vi) 4,1
Let the polynomial be ax2 +
bx + c, and its zeroes be α and β
Page No: 36
Exercise 2.3
1. Divide the
polynomial p(x) by the polynomial g(x) and find the quotient and remainder in
each of the following:
Answer
(i) p(x) = x3 - 3x2
+ 5x – 3, g(x) = x2 - 2
If a = 3, then b = -3√2, c = 1
Therefore, the quadratic polynomial
is 3x2 – 3√2x + 1.
(iii) 0, √5
Let the polynomial be ax2 +
bx + c, and its zeroes be α and β
α + β = 0 = 0/1 = -b/a
αβ = √5 = √5/1 = c/a
if a = 1, then b = 0, c = √5
Therefore, the quadratic polynomial
is x2 + √5.
ALSO READ:
(iv) 1, 1
Let the polynomial be ax2 +
bx + c, and its zeroes be α and β
α + β = 1 = 1/1 = -b/a
αβ = 1 = 1/1 = c/a
if a = 1, then b = -1, c = 1
Therefore, the quadratic polynomial
is x2 –x + 1.
(v) -1/4, 1/4
Let the polynomial be ax2 +
bx + c, and its zeroes be α and β
α + β = -1/4 = -b/a
αβ = 1/4 = c/a
if a = 4, then b = 1, c = 1
Therefore, the quadratic polynomial
is 4x2 + x + 1.
(vi) 4, 1
Let the polynomial be ax2 +
bx + c, and its zeroes be α and β
α + β = 4 = 4/1 = -b/a
αβ = 1 = 1/1 = c/a
if a = 1, then b = -4, c = 1
Therefore, the quadratic polynomial
is x2 - 4 x + 1.
Page No: 36
Exercise 2.3
1. Divide the polynomial p(x) by the
polynomial g(x) and find the quotient and remainder in each of the following:
Answer
(i) p(x) = x3 - 3x2
+ 5x – 3, g(x) = x2 - 2
Quotient = x-3 and remainder 7x-9
(ii) p(x) = x4 – 3x2
+ 4x + 5, g(x) = x2 + 1 - x
Quotient = X2 + X – 3 and remainder 8
(iii) p(x) = X4 –
5X + 6, g(X) = 2 – X2
Quotient = −x2 −2 and remainder −5x + 10
2. Check whether the
first polynomial is a factor of the second polynomial by dividing the
Second polynomial:
Answer
(i) t2- 3, 2t4 + 3t3
– 2t2 – 9t – 12
t2 – 3 exactly divides 2t4 +
3t3 – 2t2 – 9t – 12 leaving no remainder, Hence it is
a factor of 2t4 + 3t3
– 2t2 – 9t – 12.
(ii) X2 + 3X + 1, 3X4 + 5X3
– 7X2 + 2X + 2
X2 + 3x + 1 exactly divides 3x4 + 5x3 − 7x2 + 2x + 2 leaving
no remainder. Hence, it is factor of 3x4
+ 5x3 − 7x2 + 2x + 2.
(iii) x3
– 3x + 1, x5 – 4x3 + x2 + 3x + 1
x3
– 3x + 1 didn’t divides exactly x5 − 4x3 + x2 +
3x + 1 and leaves 2 as remainder.
Hence, it is
factor of x5 − 4x3
+ x2 + 3x + 1.
3. Obtain all other zeroes of 3x4 + 6x3 – 2x2 – 10x – 5, if two
of its zeroes are √(5/3).
Answer
p(x) = 3x4
+ 6x3 – 2x2 – 10x – 5
Since the two zeroes are √(5/3) and − √(5/3)
3x4 + 6x3 – 2x2 – 10x
– 5
Therefore, we divide
the given polynomials by x2 − 5/3
3x4
+ 6x3 − 2x2 − 10x – 5 =
We factorize x2
+ 2x + 1
= (x + 1)2
Therefore, its zero is
given by x + 1 = 0
X = -1
As it has the term
(x+1)2, therefore, there will be 2 zeroes at x = −1
Hence, the zeroes of
the given polynomial are √(5/3) and −√(5/3), −1 and −1.
4. On dividing x3−3x2+x+2 by a
polynomial g(x), the quotient and
remainder were x−2 and
−2x + 4, respectively.
Find g(x).
Answer
Here in the given
question,
Dividend = x3−3x2+x+2
Quotient = x – 2
Remainder = −2x + 4
Divisor = g(x)
We know that,
Dividend = Quotient x Divisor + Remainder
= x3−3x2+x+2 = (x−2)
x g(x) + (−2x + 4) = x3 – 3x2 + x + 2 –
(-2x + 4) = (x – 2) x g(x)
= x3−3x2+3x−2 = (x−2)x
g(x)
=
g(x) = (x3−3x2+3x−2)/(x
−2)
So, g(x) = (x2−
x+2)
5. Give examples of polynomial p(x), g(x), q(x)and r(x), which satisfy the division algorithm and
(i) deg p(x) = deg
q(x)
(ii) deg q(x)
= deg r(x)
(iii) deg r(x)
= 0
Answer
(i) Let us assume the division of 6x2 + 2x + 2 by 2
Here, p(x) = 6x2 + 2x + 2
g(x) = 2
q(x) = 3x2
+ x + 1
r(x) = 0
degree of p(x)
and q(x) is same i.e. 2.
Checking for division algorithm,
P(x) = g(x) x
q(x) + r(x)
Or, 6x2
+ 2x + 2 = 2x(3x2 + x +1)
Hence, division algorithm is satisfied.
(ii) Let us
assume the division of x3 +
x by x2,
Here, p(x) = x3
+ x
g(x) = x2
q(x) = x and r(x) = x
Clearly, the degree of q(x) and r(x) is the same i.e.1.
Checking for division algorithm,
p(x) = g(x) x
q(x) + r(x)
x3 +
x = (x2) x x + x
x3 +
x = (x3) + x
Thus, the division algorithm is satisfied.
(iii) Let us assume the division of x3+1 by
x2.
Here, p(x) = x3 + 1
g(x) = x2
q(x) = x and r(x) = 1
Clearly, the degree of r(x) is 0.
Checking for division algorithm,
p(x) = g(x) x
q(x) + r(x)
x3 + 1 = (x2) x x + 1
x3 +
1 = (x3) + 1
Thus, the division algorithm is satisfied.
Exercise
2.4
Verify that
the numbers given alongside of the cubic polynomials below are their zeroes.
Also verify
the relationship between the zeroes and the coefficients in each case:
(ii) x3
– 4x2 + 5x – 2; 2,1,1
Answer:
(i) p(x) = 2x3
+ x2 – 5x + 2.
=0
P(-2) = 2(-2)3 + (-2)2 – 5(-2) + 2
= -16 + 4 + 10 + 2 = 0
Therefore
1/2, 1 and -2 are the zeroes of the given polynomial.
Comparing
the given polynomial with ax3+
bx2 + cx + d, we obtain a = 2,
b = 1,
c = -5, d = 2
We can
take α = 1/2, β = 1, ƴ = -2
Therefore, the relationship between the zeroes and the
coefficients is verified.
(ii) p(x) = x3
– 4x2 + 5x – 2
Zeroes for this polynomial are 2,1,1.
P(2) = 23 –
4(22) + 5(2) – 2
8 – 16 + 10 – 2 = 0
p(1) = 13 –
4(1)2 + 5(1) – 2
= 1 – 4 + 5 – 2 = 0
Therefore 2,1,1 are the zeroes of the given
polynomial.
Comparing the given polynomial with ax3 + bx2 + cx + d, we
obtain a = 1, b = -4, c = 5, d = -2.
Verification of the relationship between zeroes and
coefficient of the given polynomial
Hence, the relationship between the zeroes and the
coefficient is verified.
Question 2:
Find a cubic
polynomial with the sum of the product of its zeroes taken two at a time, and
the product of its zeroes as 2, -7, - 14 respectively.
Answer:
Let the polynomial be ax3 + bx2 + cx + d and the zeroes be α, β and
ƴ
If a =
1, then b = -2, c = -7, d = 14
Hence, the polynomial x3 - 3x2 + x + 1
are a-b, a, a+b, find a and b.
Answer:
p(x) = x3 - 3x2
+ x + 1
Zeroes
are a – b, a + a + b
Comparing
the given polynomial with px3
+ qx2 +rx + 1, we obtain
P = 1,
q = -3, r = 1, t = 1
Sum of
zeroes = a – b + a + a + b
The zeroes are 1 – b, 1, 1 + b.
Multiplication of
zeroes = 1(1-b)(1+b)
|
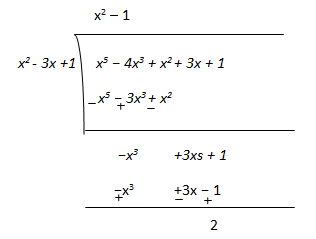
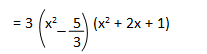
Comments
Post a Comment
paliyal education IMPORTANT: All the contents of this Blog is for educational and informational Purpose only. All over internet owner self - made in good faith, makes an effort to become a helpful platform for learn Astrology and new youtubers